相関係数を乱数シミュレーションしよう

シミュレーションファイルは、Excel 97 形式です。

圧縮なし （151KB）　※ お使いのブラウザによっては、直接開けます。
LZH 形式による圧縮 （53KB）

解説

Ｘ, Ｙ は独立な標準正規乱数とします。このとき、
　　
とおくと、U, V の相関係数は ρ（ギリシャ文字の”ロー”, rho）となります。

「シミュレーション」ワークシートのセル B3 に、-1 から 1 までの任意の数値（rho）を入力してみてください。「データ」ワークシートに U, V の値が出てきます。これが求める乱数です。

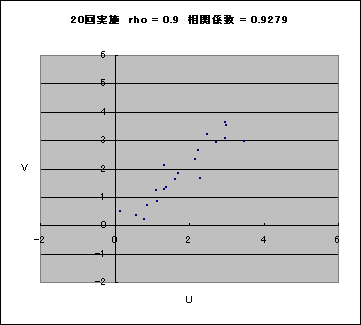
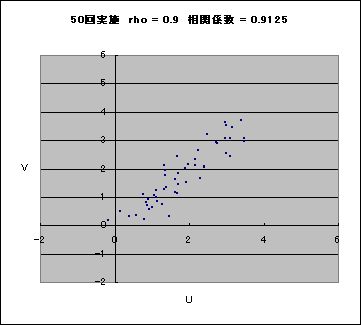
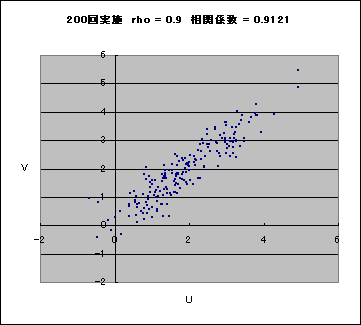
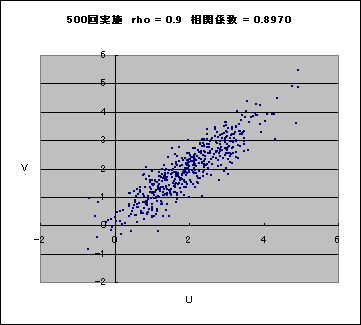
実際の相関係数はこれに近いはずです。20, 50, 200, 500 と試行回数が多くなると、全体によくなるはずです。「シミュレーション」ワークシートの 4 枚の散布図と、そのタイトルに表示されている相関係数の値を見比べてみてください。なお、U, V ともに正規分布 N(2, 1) に従っています。

標準正規乱数を改めて生成すると、また別の U, V が導出され、散布図の形や相関係数も変わってきます。F9 キーを押すとワークシート全体が再計算されますので、これを確かめることができます。F9 を何回も押してみましょう。ある程度のばらつきはありますが、おおむね最初に B3 に入力した rho の値の近くに収まるはずです。

相関係数について詳しくは、こちらをご覧ください。

補足：このシミュレーションプログラムを自作したい人のためのヒント

• Excel で標準正規乱数を生成するには、標準正規累積分布関数の逆関数を返す「NORMSINV」関数と、[0,1] 一様乱数を発生させる「RAND」関数を使って、「=NORMSINV(RAND())」と入力します（「データ」ワークシートの B, C 列）。
• 4 つのグラフのタイトルは、C7:C10 のそれぞれのセルに連動して変わるようになっています。今回のように F9 を押すことによって何回もシミュレーションを繰り返す場合、これは便利な方法です。グラフのタイトルをクリックして、数式バーに「=C7」など参照したいセル番地を入力し、Enter を押します。
• 上記方法で参照できるのは 1 つのセルのみであるため、そのセルにすべての必要な情報を集約できるように、C7:C10 では文字列演算式を使っています。
• 「シミュレーション」ワークシートでは、セル B3 以外を変更できないようにシート保護をかけてあります。これを解除するには、[ツール]−[保護]−[シート保護の解除...] を実行します。

散布図のサンプル

rho = 0.9 とした場合の実現値の一例

　無相関の場合の密度関数（３Ｄグラフ）　=>　ここ