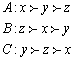
である。
(i) x, y, z に対する一対比較の多数決による社会的決定は「投票の逆理」を
もたらすことを示しなさい。
(ii) これに対し、まずある二者の多数決の勝者と残り一者とを多数決で決
する社会的決定にも問題があることを示しなさい。
松原(望)教官 「計量社会科学」試験 1998.2
教科書(指定ずみ)、自筆ノート、電卓 : 持ち込み可
ノート・コピー :持ち込み不可
5問を選択。解答はなるべく番号順とすること。
1. A, B, C 3 人の選択肢 x, y, z に対する選好は
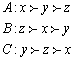
である。
(i) x, y, z
に対する一対比較の多数決による社会的決定は「投票の逆理」を
もたらすことを示しなさい。
(ii)
これに対し、まずある二者の多数決の勝者と残り一者とを多数決で決
する社会的決定にも問題があることを示しなさい。
2. 利得行列
![]()
による 2
人零和ゲームが混合戦略(純粋戦略でない)の最適戦略を持つ条件を
述べ、各プレーヤーの最適混合戦略、その最適値(maxmin 値、
minmax 値)を
求めなさい。
3. 利得行列
![]()
を持つ 2
人非零和ゲームにおいて、とられる行動を予想し、それを保証する
条件について述べなさい。
4. ロトカ・ヴォルテラのモデルを
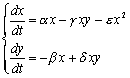
のように修正しよう。
(i) その意味は何か。
(ii)
定常均衡点(運動の消失点)で正のものがある条件を求めなさい。
5. (i) -1 < a < 1のとき
(1-a) -1 = 1 + a + a2 + a3 +
・・・
を示しなさい。ただし、形式的(収束自体の証明は不要)でよい。
(ii) 正方行列 A に対し、ある条件のもとで
(I-A) -1 =I + A + A2 + A3 +・・・
となることの形式的証明を与え、A
が産業連関表の投入係数行列である
ときのこの式の意味を述べなさい。
[ヒント] 収束するとし右辺を s として as
6. 線形計画法の最適化問題:
条件
x + y +3z≧2
2x + y + z≧1
x≧0, y≧0, z≧0
のもとに
14x + 8y + 18z
を最小化
の最適値(最小値)を求めなさい。
レ ポ ー ト 出 題
「計量社会科学ホーム・ページ」から、練習問題 No.15-23 より 3 問を解く。なお、正誤表も参照。
締め切り 2月末日
提出場所 教務課
※ 提出者には評価に応じ、最高 25 点を試験点数に加点する。