問題
dx / dt = x （x (0) = 1, 0 <= t <= 1）
数値解
◎ 刻み幅 h = 0.1 のとき
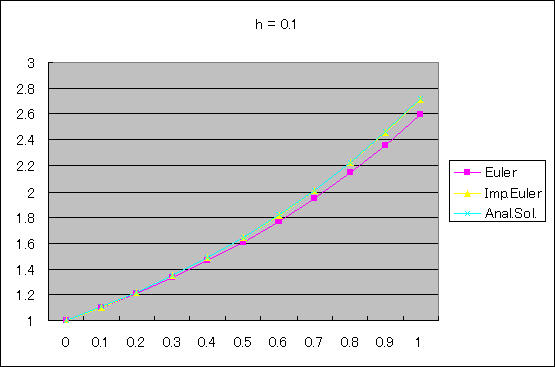
Euler ： オイラー法による数値解
Imp.Euler ： 改良オイラー法による数値解
Anal.Sol. ： 解析解（x = exp(t)）
◎ 刻み幅 h = 0.01 のとき
dx / dt = αx
x = C exp (αt) （C は積分定数）
問題
dx / dt = x （x (0) = 1, 0 <= t <= 1）
数値解
◎ 刻み幅 h = 0.1 のとき
Euler ： オイラー法による数値解
Imp.Euler ： 改良オイラー法による数値解
Anal.Sol. ： 解析解（x = exp(t)）◎ 刻み幅 h = 0.01 のとき
微分方程式の数値解法
へ戻る