ロトカ・ヴォルテラ モデル

モデル

dx / dt =  αx - γxy　　（被食者）
dy / dt = -βy + δxy　　（捕食者）

解析解

αlog y - γy = -βlog x + δx + C　　（C は積分定数）

解曲線の x - y プロット図

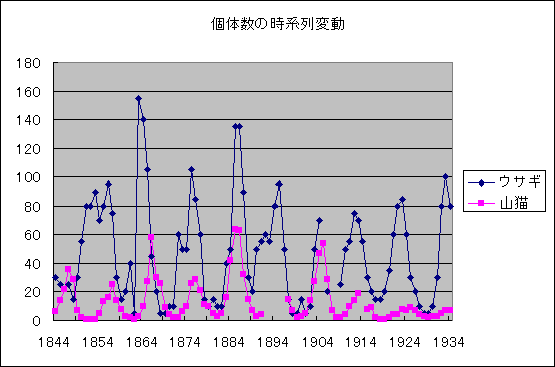
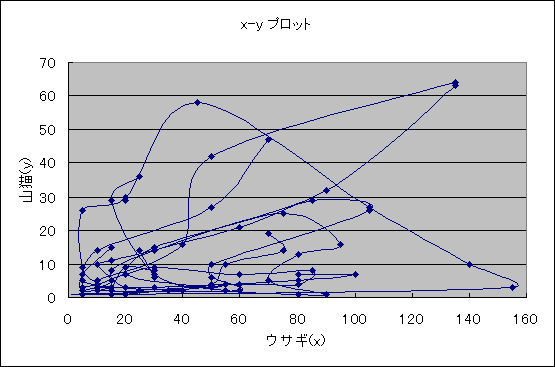
I） パラメータ群を
　　α = 5,
　　β = 3,
　　γ = 2,
　　δ = 2
とし、積分定数 C を -10（一番外側）から -3（一番内側）まで 1 刻みで動かしたときの解曲線群

※ Mathematica の以下のコマンドにより描画

<< Graphics`ImplicitPlot`;
ImplicitPlot[
　　Table[5Log[y] - 2y == -3Log[x] + 2x + c, {c, -10, -3}]
　　// Evaluate, {x, 0.1, 20}, {y, 0.1, 15}, PlotPoints -> 100]

II） パラメータ群を
　　α = 5,
　　β = 3,
　　γ = 7,
　　δ = 2
とし、積分定数 C を -16（一番外側）から -9（一番内側）まで 1 刻みで動かしたときの解曲線群

データ例

カナダオオヤマネコ と カンジキウサギ の 1844 〜 1934 年の個体数変動

データはこちら（Excel 形式）

微分方程式の数値解法 へ戻る