![]() 解説は第
5 章第 5 節
解説は第
5 章第 5 節
Wolfram Research, Inc. の数学ソフト Mathematica によるシミュレーションの例です。
ボールド体の文字列は、Mathematica に入力するコマンドを表します。ノーマル体の文字列は筆者のコメントを表します。この色の部分は、Mathematica のコマンドについての解説です(Mathematica をご存知の方は飛ばしてかまいません)。
※ 東京大学の学生のみなさんへ
Mathematica は ECC の X 端末で利用できます。kterm からは「math」と入力すればターミナル版が起動します。また、アプリケーションサーバーに接続すれば、フロントエンド版も使えます。
![]()
最初にロジスティック写像 y = r x (1 - x) を定義します。「lambda」とは左の式でいう r にあたります。
点列 x0, x1, x2, ・・・ がどのように変化していくかを見てみましょう。テキスト p.198 の図 5.22a にあたります。
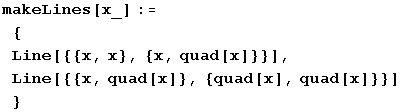
対角線 y = x 上の点 (x, x) から曲線 y = r x (1 - x) に垂線を引くとともに、その交点から再び対角線 y = x に水平線を引く関数を定義します。
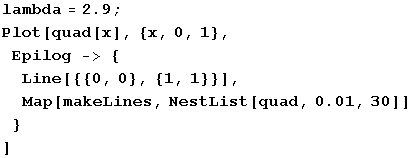
まず、lambda が 2.9 のときを考えてみましょう。
入力式中、「Epilog」オプションはまず本体のグラフを描画してから別のグラフを上書き追加するためのもの、「Map」関数は第 1 引数(この場合「makeLines」)を、第 2 引数(「NestList [quad, 0.01, 30] 」)から導出されるリストに順次適用するものです。
NestList [f, expr, n] は、式もしくは数値 expr に 関数 f を、最初の n = 0 (つまり何も適用しないもとの値)を含めて、n + 1 回適用したリストを返します。たとえば、NestList [f, x, 3] は、{ x, f [x], f [f [x]], f [f [f [x]]] } というリストを返します。上の入力式中の「NestList [quad, 0.01, 30]」はしたがって、0.01から出発して quad を順次適用した、31 個の数値のリストを返します。
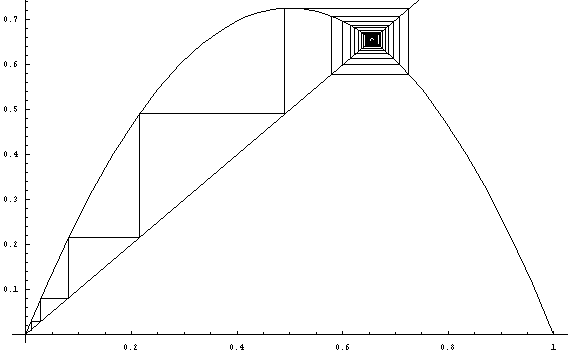
点列の行き先(クモの巣のようなもの)が時間が経つにつれて 1 点に収束する様子が分かります。しかもその点は対角線 y = x 上にある、すなわち不動点であることに注意してください。
【研究 1】 x の初期値(この場合 0.01)を変えてみたらどうなるでしょうか。
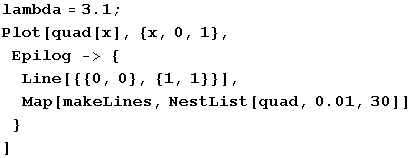

次に lambda の値を 3.1 に変えてみましょう。他の条件はすべて同じであるにもかかわらず、点列の収束先が四角形になっている様子が分かります。このうち対角線上の 2 点は作図上の便宜のためのものですから、実際の x の値は収束先の四角形の左上および右下の 2 点を交互にとっていることになります。つまり 2 周期点です。
【研究 2】 この場合の収束先の値はそれぞれいくつになりますか。後出の「NestList」と「Nest」を組み合わせた方法で、計算してみてください。
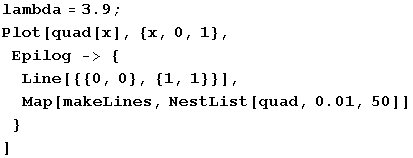
lambda の値をさらに変えて 3.9 にしてみましょう。今度は上の 2 つと違い、どこかに収束しそうな様子はありません。これがカオスです。
上記 3 つのケースの違いを考えるために、lambda の違いによる x の行き先の値の変化を見てみましょう。
なお、以下で考える x の値は、繰り返しの回数が十分多くなって x の出方がある程度落ち着いてきた時点から先のものです。つまり、最初の x の値によらない議論になります。
![]()
お使いのコンピュータの環境によっては、繰り返し計算をする際のレベルが一定値に制限されていて、以下の計算をする際にエラーが出ることがあります(少なくとも、筆者のテストした環境(64 MB RAM, Windows 95, Mathematica 3.0)ではエラーになりました)。
この場合、上のコマンドを入力するとうまく計算できることがあります。
ただし、環境によっては他のアプリケーションやオペレーティングシステムに悪影響を与えるかもしれませんので、ご注意ください。

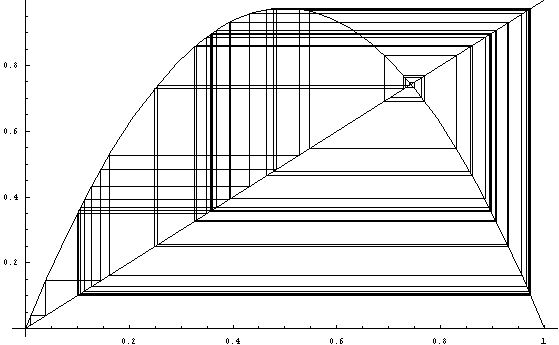
lambda を 0 から 4 まで 0.01 きざみで動かしたときに x の値がどうなるかを見てみましょう。ここでそれぞれの lambda について、x は初期値 x0 = 0.5 から始めたときの、x500 から x628 までをプロットしてあります。
この入力式は複雑に見えますが、一つ一つ丹念に見ていけば難しいことはありません。
まず、「Table [lambda, {129}]」は、{lambda, lambda, ・・・, lambda} という lambda が 129 個含まれたリストを生成します。
次に「NestList [quad, Nest [quad, 0.5, 500] , 128]」の部分ですが、これは先ほどの「NestList」の第 2 引数に単なる数値ではなく、他の関数によって生成される数値をとったものです。その関数「Nest」は、「NestList」と似ていますが、後者が f を n 回繰り返したときのすべての値をリストの形で返すのに対し、前者は n 回適用したときの最終結果だけを返します。つまり、「Nest [quad, 0.5, 500]」とは、ロジスティック写像を f (x) とすれば、f 500(0.5) を意味します。従ってこの「NestList」の全体は、x500 から x628 までの 129 個分の数値のリストを返します。
この 2 つのリストに対して、「Transpose」を適用することにより、行列における転置のような操作ができます。つまり、それぞれ 129 個の要素からなる 2 つのリストを、それぞれ 2 つの要素からなる 129 個のリストに変換します。具体的に言えば、{ {lambda, lambda, ・・・, lambda}, {x500, x501, ・・・, x628} } というリストを、{ {lambda, x500}, {lambda, x501}, ・・・, {lambda, x628} } というリストに変換します。
その次のレベルにかかる「Table」は、lambda を 0 から 4 まで 0.01 きざみで動かしたときにそれぞれ「Transpose」内を計算した結果をリストとして返します。つまりこの段階で、{ { {0, x500}, ・・・, {0, x628} }, { {0.01, x500}, ・・・, {0.01, x628} }, ・・・, { {4, x500}, ・・・, {4, x628} } } というリストが生成されています。
「Flatten」関数は、このリストのうち第 1 のレベルの括弧を取り外します。この段階でやっと、{ {0, x500}, ・・・, {0, x628}, {0.01, x500}, ・・・, {0.01, x628}, ・・・, {4, x500}, ・・・, {4, x628} } という 129 x 401 = 51,729 個(!)の、2 つの要素からなるリストのリストができます。
最後に「ListPlot」がこの 51,729 個のリスト(=この場合は 2 次元座標上の点)について、それぞれ第一要素を x 座標、第二要素を y 座標とみなし、プロットしていきます。
以上のことから想像できるように、この計算は非常に時間がかかります。筆者の環境(Pentium Pro 200 MHz, 64 MB RAM, Windows 95, Mathematica 3.0)でも 54 秒かかりましたので、気長に待ちましょう。
テキスト pp. 199-200 の記述が確かめられると思います。

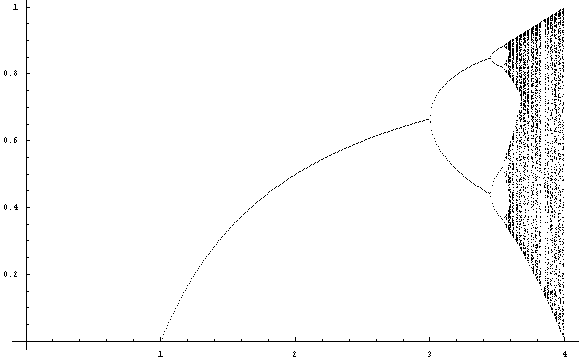
次に r の範囲を 3 から 4 に狭めて、もっと詳しく見てみましょう。
先ほどの入力式が理解できれば、今度の式も容易に理解できるはずです。今回は先ほどの約 2 倍のリストを生成していますので、さらに時間がかかります。筆者の環境で 1 分 38 秒かかりました。
テキスト p. 190 の図 5.23 の上の図にあたります。周期倍分岐の様子や、窓(3.828427 < r < 3.841499)の存在が確認できるでしょう。

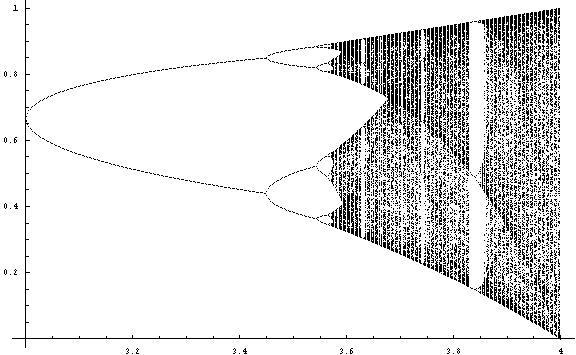
最後に上の図の「窓」の近辺をもっと拡大してみましょう。
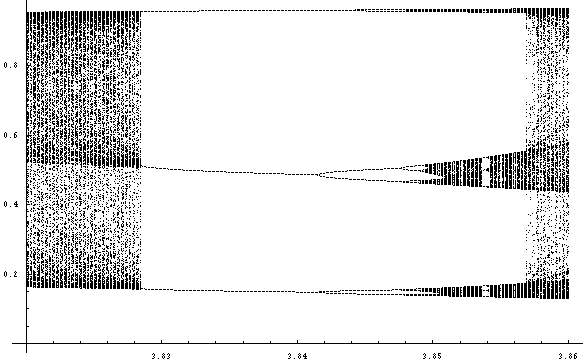
「窓」の後に分岐図全体を縮小したようなものが再び現れることがわかります。これは、ロジスティック写像のもつ自己相似性によるもので、フラクタルに通じます。
【研究 3】 入力式のパラメータを変えて、小さい窓をさらに拡大していってみてください。
※ このシミュレーション例の作成にあたっては、Theodore W. Gray, Jerry Glynn, Explorering Mathematics with Mathematica, Addison-Wesley Publishing Company, Inc., 1991. (時田節、藤村行俊訳『Mathematica 数学の探索』株式会社トッパン、1994)を参考にしました。