2002年度 計量社会科学
第4回レポート(社会システム)
7月8日出題、8月2日提出(訂正)
提出法
修正履歴
7/11 3 訂正(定数項を 1 から x へ)
7/12 9 ii) 保留解除
2 vii) 出題
10 出題
7/23 5 ii) 出題
4 iii) ヒント追加
7/25 提出法
<基礎学力>
1 【数列】 次の数列の第 20
項まで求め、図示しなさい。また有限の極限値のあるものについてはそれを求めなさい。
i) 初項 10, 公差=3 の等差数列
ii) 初項 2, 公比=0.7 の等比数列
iii) an+1= 0.8 an+ 3.2, a1=
10
<ヒント> i) では A1 に 10 と入れ、A2 に「=A1+3」と入れて、リターンキー。A2
の右下の小■印にマウス・ポインタを合わせて、下へドラッグ(命令の複写)。グラフはツールバーのグラフ・ウィザードから。折線グラフを選ぶ。→
データ範囲を指定してから。
2 【関数グラフ】
次の関数のグラフを描きなさい。(かっこ[ ]内は計算に際しての
x の変化幅。これより細かくてもよい)
i) 正弦関数 sin x (0 〜 2π) [0.05]
ii) 余弦関数 cos x (0 〜 2π) [0.05]
iii) 同、位相ずれ 3 sin 2x+4 cos2x (0 〜π) [0.01]
iv) 指数的発散 e2x (0 〜 3) [0.01]
v) 指数的減衰 e-x ( 0 〜 5 ) [0.05]
vi) 減衰振動 e-x sin2x (0 〜 5) [0.05]
vii) ロジスティック関数 5/(1+2 e-t/2) (-10
〜 10) [0.1]
<ヒント> i) A1, A2,… に x を入れ、B1
には関数ウィザード(ツールバー)fx から SIN
を選んで入れる。自動的に=が付き、数値入力窓(ダイアログボックス)が表示されるので、ボックスの右下赤印をクリック、データ範囲を指定(再び赤印クリック)するか、自ら
A1:A130 などのように手入力する。最後は OK
とする。あとは 1 と同様にドラッグして完成。iii)
は 2 行を加える。 
 授業板書
授業板書


3 【微分方程式】 次の微分方程式の解 x(t)
を求め、適当に図示しなさい。
6 d2x/dt2− 5 dx/dt + x = 0
初期条件: t=0 のとき、x=5, dx/dt=2
<ヒント> p.176 [定理2]
4 【行列演算:逆行列】
逆行列について学びなさい。また、次の i), ii)
の逆行列を求めなさい。さらに iii)
の連立方程式を解きなさい。
i) 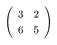 (筆算で)
(筆算で)
ii) 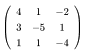 (EXCEL で)
(EXCEL で)
iii) 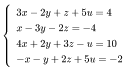 (逆行列の方法およびクラメールの公式で)
(逆行列の方法およびクラメールの公式で)
<ヒント>
巻末「行列と行列式(線形代数)」まとめ。ii) は EXCEL
で MINVERSE。上記 2 ヒント参照。ただし「OK」用いない。iii)
で、行列式は MDETERM 使用。
5 【行列演算:固有値問題】
正方行列の固有値問題について学び(p.181 下段)、次の i),
ii)
の対称行列の固有値問題を解きなさい。ベクトルは長さ 1
とすること。
i) 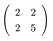 (計算で)
(計算で)
ii) 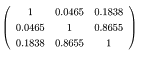 (固有値プログラム使用)
(固有値プログラム使用)
<ヒント> 最大固有値は 1.8953,固有ベクトルは(0.1800,
0.6885, 0.7025)’ etc.
<方法応用>
6 2,000 万円の融資を年 3.75% の利率で受けるとき、15
年で返済するための割賦の年額を求めなさい。また、各年の残債を求めなさい。
<ヒント> 1 iii) と同形式。
7 p.169の a), b), c), d)
の差分方程式の解(人口爆発、個体数の安定、漸近的減少の例など)を第
5 項まで求めなさい。初期条件は図 5.7 とする。
8 次の需要関数・供給関数
d=2.5−0.85p, s=0.05+0.6p
に対し、「くもの巣」モデルを計算し図示しなさい。p=2.8
で、まず生産者が行動する。
<ヒント> pp.161, 162, 1 iii) と同形式。
9
i) リチャードソンのモデルでドイツ vs.フランスのケース
dx/dt=−18x+4y
dy/dt= 4x−10y
の一般解(x(t), y(t))を求めなさい。係数は小数点以下 2
桁とする。
<ヒント> (3.8)−(3.11)にならう。
ii)
ロトカ・ヴォルテラの被食者・捕食者モデル
dx / dt = αx - γxy (被食者)
dy / dt = -βy + δxy (捕食者)
において、パラメータ群の 2 ケース
i) α = 5, β = 3, γ = 2, δ = 2
ii) α = 5, β = 3, γ = 7, δ = 2
に対する解曲線の
x-y プロット図 I, II を見て、特色を比較しなさい。
10 ベルタランフィーの一般システム論でいう「前進的分離」とはなにか。式を用いて説明しなさい。また全体性、総和性とは何か。
<ヒント> p.187
※ 提出法、2年生締切は別途通知。
 レポート一覧
レポート一覧
![]()
![]() 授業板書
授業板書
![]()
![]()
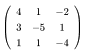 (EXCEL で)
(EXCEL で)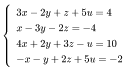 (逆行列の方法およびクラメールの公式で)
(逆行列の方法およびクラメールの公式で)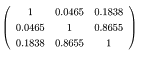 (
(