 |
 |
|
|
|
|||
| 下記解 I, II 参照 | 下記解 III 参照 |
『入門確率過程』の裏カバーに例を表示
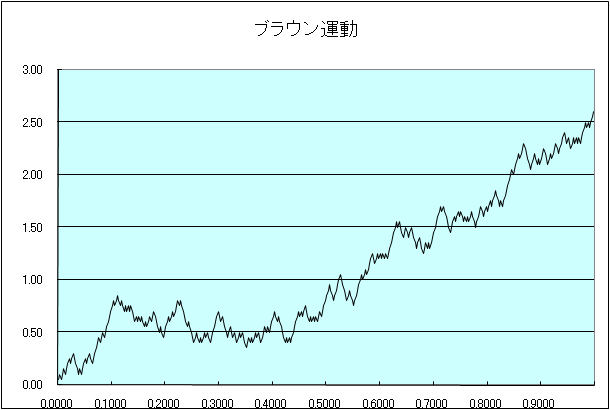
「ランダム・ウォーク」から「ブラウン運動過程」を生成するシミュレーション実験を次の方法で行いなさい：
以下の離散乱数を 100 回生成させ、1 回目、2 回目までの和、3 回目までの和、・・・、100 回目までの和（累積和、部分和）を計算し、それを横軸にとった 0.01, 0.02, 0.03, ・・・, 1.00 に対してプロットする。=> EXCELでは、SUBTOTAL を利用。
| 空間幅（運動の幅） | ±0.1 | （Δx = 0.1） | ||
| 離散乱数 | ||||
| 値 | 0.1 | - 0.1 | ||
| 確率 | 0.6 | 0.4 | （0.5 ± 0.1） | |
| 時間幅 | 0.01 | （Δt = 0.01） | ||
| 全時間 | 0 から 1 | （100 回分） |
次のようにパラメータを変えて、I と同様の実験をしなさい。
| 空間幅（運動の幅） | ±0.05 | （Δx = 0.05） | ||
| 離散乱数 | ||||
| 値 | 0.05 | - 0.05 | ||
| 確率 | 0.55 | 0.45 | （0.5 ± 0.05） | |
| 時間幅 | 0.0025 | （Δt = 0.0025） | ||
| 全時間 | 0 から 1 | （400 回分） |
* 時間 0 では位置も 0 とする。
* 時間幅 Δt は空間幅 Δx の 2 乗であるが、一般には Δx の 2 乗に比例すればよい。確率は 0.5 ± Δx となっているが、一般には 0.5 ± k Δx（k は定数）でよい。いずれも、同種ではあるが少しずつ異なった様子のブラウン運動が生じる。
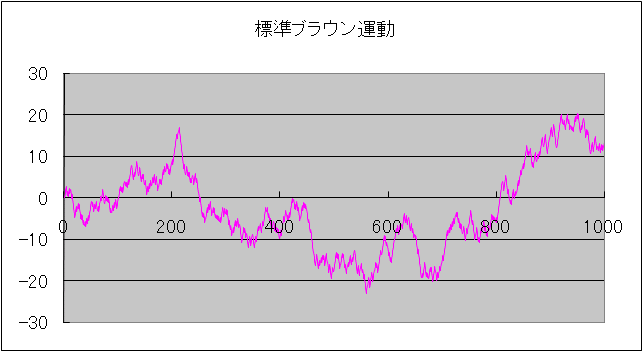
II を、平均 0, 分散 t となるように、尺度の線形変換をする。
下記の解を参照。
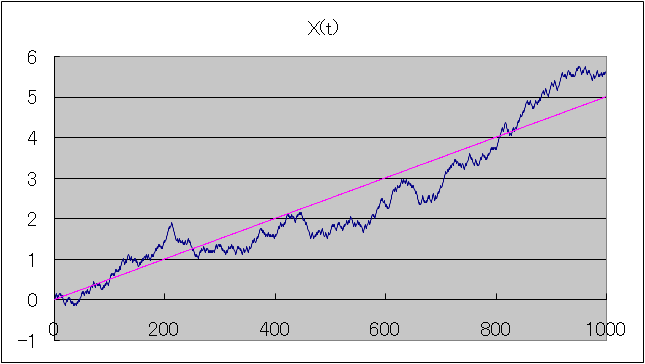
III を 2 通り作成、横軸・縦軸にプロットする。
作成中
I, II ランダム・ウォークのシミュレーション
III 標準ブラウン運動（ランダム・ウォーク X(n) で近似後、線形変換）
東京図書作成（承認済み）
IV ２次元標準ブラウン運動（ファイルサイズ注意(2,286KB)！ZIP形式(536KB)もあります）
１次元のものを 2 個作り組み合わせる。
東京図書作成（承認済み）