練習問題

※　［解答方針］がこちらにあります。
※　《optional》とあるのは研究です。
※　これは、各概念の本質をついた問いというよりも、むしろそれが理解できていないとできない問題ばかりです。

【第1章理解】次の重要語句を学び、後の各問につき 200 字程度で答えなさい。

　　　「つつき順序」(1)、「選好順序」(7)、「効用」(11, 12)、「効用の個人間比較の禁止」(24)、
　　　「パレート原理」(24)、「リベラル・パラドックス」(4, 25)　
　　 ( )内はページ。

ある 2 状態 x, y の比較（効用の比較）

　 x（現状） y（新政策）

A 12 11.5

B 2 10

（テキスト p.25）

とそれらの選択の問題を題材（例）に、次の場合を論じなさい。

(i) A, B 間に動物社会にみられるような「つつき順序」があるとき
(ii) A, B の効用が比較できるとき
(iii) 同じく比較できないとき
(iv) これらの場合に関連して、セン（A. Sen）の次のことばが意味するところを述べ、あなたの考えを述べなさい。

　　「パレート主義者は開発途上国に来てその貧困を前にしたとき、言葉を
　　失うだろう。」

(v) パレート原理はほんとうに「自由」の原理か。
【第1章理解】アローによる民主的社会厚生関数の不可能性の公理中、「非独裁」の内容を論理的にきちんと述べて下さい。（論理記号は巻末付録を参照）
【パレート最適】囚人のジレンマにおいて (C, D), (D, C) がパレート最適であることを示しなさい。
【パレート原理】あなたはパレート原理に賛成ですか。
　　ヒント： Sen, "Impossibility of Paretian Liberal" を読む。
【リベラル・パラドックス】リベラル・パラドックスにおいて、「好き者」の順序につき解説しなさい。
【自由】数理的方法で「自由」を扱うことの適否、是非を論じなさい。
【安心ゲーム】「安心ゲーム」で「安心」できる理由をあげなさい。
【無差別曲線】テキストの無差別曲線を持つ消費者が予算制約 3x + 4y = 120 のもとで行う最適な決定 (x, y) を求めなさい。
【戦略】
(a) 戦略と戦術の関係およびその説明例を与えなさい。
(b) [問題文が長いので別のページにリンク]
【投票】「投票のパラドックス」が起きない例を挙げなさい。

【 2 人ゼロ和ゲーム】《optional》次の 2 人ゼロ和ゲームがある。

	β₁	β₂	β₃
α₁	6	-2	3
α₂	-4	5	4

i)		純粋戦略ではナッシュ均衡点はないことを示しなさい。
ii)		プレーヤー I のマクスミン混合戦略を求めなさい。マクスミン値はいくつか。
iii)		ii) を考えるにあたり、プレーヤー II は β₃ をとることは除外してよいことを示しなさい。
iv)		iii) から II は β₃ を用いない。このことから、II のミニマックス戦略を求めなさい。ミニマックス値はいくつか。

【協力の可能性】「チキン」と「囚人のジレンマ」で自発的協力はどちらが可能性が高いか。
【ナッシュ均衡】「チキン」「両性の闘い」におけるナッシュ均衡を求め、その理由を言いなさい。
【ナッシュ均衡】国際政治のゲーム（テキスト pp. 34-35, 51-53, ただし、ここでは効用値の大きい順に 1, 2, 3, 4 と順位づけしてある）において、ナッシュ均衡があればそれぞれ求めなさい。
【裏切りの可能性】囚人のジレンマ (表 6.3) をおのおの図示し、裏切り D の起こりやすさを論じなさい。
【展開型ゲームの最適戦略】

i) 「硬貨あわせゲーム」（図 2.7）の展開型ゲームで表の確率を p = 3/5、裏の確率を q = 2/5として、パス（放棄）するか否かの最適戦略をおのおの求めなさい（図の訂正あり）。
ii) このゲームはプレーヤー 1, 2 のどちらにとって有利か。

【コア】土地利用の 3 人ゲームで特性関数 v(・) の他の値（下記参照）に対し、「コア」を計算しなさい。

K	v(K)
φ	0
F	100,000
M	0
S	0
FM	220,000
FS	280,000
MS	100,000
FMS	300,000

【確率計算】

i) ポーカー・ゲームにおいて｢ツー・ペア｣が起こる確率を計算しなさい。
ii) ロイヤル・ストレート・フラッシュの確率も計算しなさい。
【ベイズの規則】｢ベイズの規則｣を用いて、症状-病名（複数）の診断モデルを作りなさい。これは｢人工知能｣ (Aritificial Intelligence, A.I.) の一つです。
【リスク・プレミアム】図 3.3 の投資をで評価した場合のリスク・プレミアムを計算しなさい。対数効用関数とどちらがリスクが大きいですか。
【アレーのパラドックス】 U (10,000) = x, U (15,000) = y, U (0) = z とおいて、「アレーのパラドックス」を説明しなさい。
【株価の利得率】銀行株データから、データに示されたこの一月の利得率（月あたり）を計算しなさい。
【リスク】表 3.13 から「リスクなくして利益なし」ということの根拠を与えなさい。図にして見ること。
【ポートフォリオと分散】分散 (3.11) を最小化するポートフォリオを求めなさい。(5), (6) の場合はどうか。また、基準 (3.12) の U との関係はどうなりますか。
【ビット】あなたが日常および学問上用いるすべての文字（漢字は除く）、記号、符号はおおよそいくつか。それは何桁の二進符号であらわされますか。
【エントロピーの性質】 104 頁にある等式
　　H ( 1/6, 1/3, 1/2 ) = H (1/6, 5/6 ) + ( 5/6 ) H ( 2/5, 3/5 )
を確かめなさい。
【熱力学の第二法則／エントロピー増大の法則】図 3.6 を参考にして、仕切りのない状態において、各 2 種の粒子 20 個ずつがもとのように左右に完全に分離した状態に戻る確率を求めなさい。
　　ヒント：極めて小さい。

　　　　　　　　　　　　　　　　　
【仮説・調査・分析】

i) 相関係数について学びなさい。
ii) ｢イデオロギー｣について知るところを述べなさい。
iii) p.147 の表 4.15 を｢イデオロギー｣という立場から解釈しなさい。
iv) アドルノのいわゆる｢権威主義的パーソナリティ｣（p.135）に関する 16 項目の各質問項目（F尺度）に 5 段階で答えなさい。
【動的システム・ 1 要素システム】次の 3 つの動的システムの共通点、相違点につき論じなさい。
　　i) 積み立て預金
　　ii) 割賦償還
　　iii) クモの巣モデル
　　iv) 等差数列
【微分方程式を解く】《optional》ロジスティック微分方程式を求積法（変数分離法）で解きなさい。
【成長曲線】ロジスティック成長においてもっとも成長の速い時点はどの時ですか。
【多要素システム／非対称関係における相互的依存】ロトカ・ヴォルテラのモデルの式において、x の大きさが y の変化に与える影響につき論じなさい。
【同／軍備の安定的均衡】リチャードソンの軍備競争モデルを用いて、表 5.3 から選んだ 2 国間の均衡軍備量の安定性を論じなさい。
【同／軍備の安定的均衡】解の安定・不安定の分類のパラメータ図（図 5.14）に、図 5.15 の軌道タイプ（ 6 種）の番号を書き入れなさい。
【分岐理論】《optional》熊手分岐（pitchfork bifurcation）とは何か。
【カオスの計算】《optional》写像
　　y = r (1 - 2 |x - 0.5| )　(0 ≦ x ≦ 1, 0 ≦ r ≦ 1)
について、ロジスティック写像と同様の計算をしてみなさい。
【カオスの計算】 A 君も B さんもそれぞれ旅をするとします。旅程はロジスティック・マップによるとし、スタート時間は 0 で、A 君は x₀ = 0.5 から、B さんは x₀ = 0.49 から出発します。十分時間が経ったとき、
　　i) r = 3.9 の場合、2 人の位置関係はどうなるでしょうか。
　　ii) r = 3.2 の場合はどうでしょうか。
計算により、あるいは理論によって確かめて下さい。
【線形計画法】《optional》次の線形計画法の解、各制約のシャドウ価格、双対問題の解を求めなさい。

条件
　　

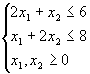
のもとに、目的関数

　　

を最大化する。
【産業連関分析】《optional》投入算出行列

　　

およびそのレオンチェフ逆行列

　　

に対して、次の最終需要に応ずる生産量を求め、これを (70, 60) に対するそれと比較しなさい。

i) (80, 60) ii) (80, 70) iii) (80, 80)

iv) (90, 80) v) (90, 90)

	x（現状）	y（新政策）
A	12	11.5
B	2	10

i)	(80, 60)	ii)	(80, 70)	iii)	(80, 80)
iv)	(90, 80)	v)	(90, 90)